図形に[3-D 回転]を設定すると、様々な角度から見た図形に変えることができます。普段使い慣れた図形でも、ひと工夫加えるだけで一歩進んだ使い方ができて面白いです。
今回の記事では[3-D 回転]の使い方と、設定した時の変化を視覚的にわかりやすくするためのサンプルをご用意しています。
また、最後に[3-D 回転]を使ったイラスト作りにもチャレンジしてみましょう。
図形の[3-D 回転]
Word、Excel、PowerPointでは、図形を三次元的に回転させることができます。

設定の基本は、[図形の書式]タブ→[図形の効果]→[3-D 回転]を使います。
[3-D 回転]の中にある既定のスタイル(標準スタイル)を選択するだけで、簡単に図形が回転します。
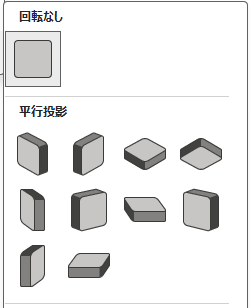
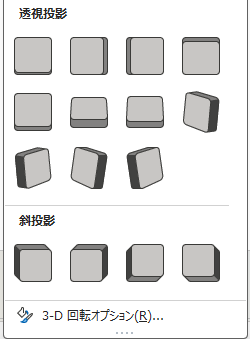
標準スタイルを選択すると、選択した回転の種類に合わせて自動的に「X、Y、Z方向」の回転値が設定されます。「3-D 回転オプション」を選択すると作業ウィンドウが開くので、そちらで確認できます。
▼ 回転なしの時
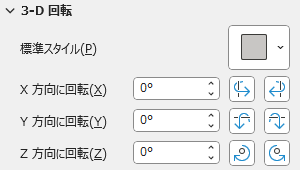
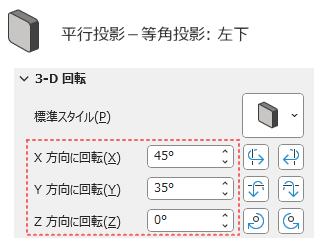
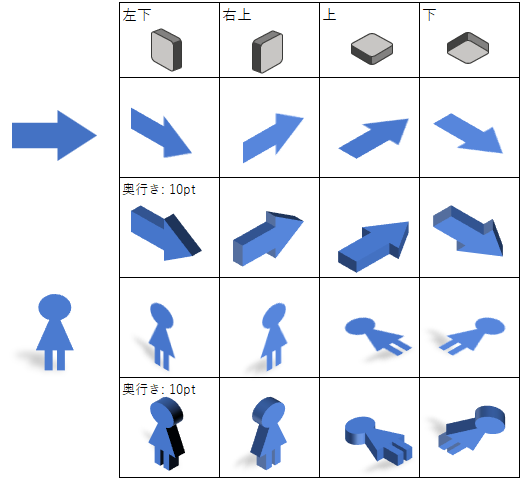
例えば、[平行投影]の[等角投影: 左下]を選択すると、「X 方向に回転」は「45度」、「Y 方向に回転」は「35度」となります。
▼ 等角投影: 左下
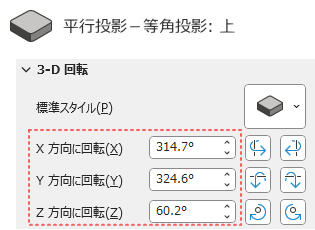
▼ 等角投影: 上
標準スタイルを使ったときに「思った回転ではないなぁ~」という時は、「3-D 回転オプション」で詳細を設定しましょう。
回転させる順序としては、
- 希望の向きに近いものを「標準スタイル」の中から選択する。
- [3-D 回転オプション]を使って微調整する。
というのが、一番混乱が少なく、作業も早いと思います。
3-Dの回転方向
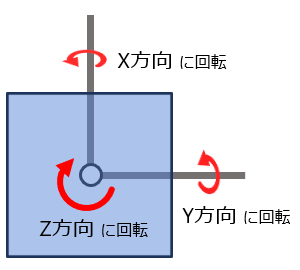
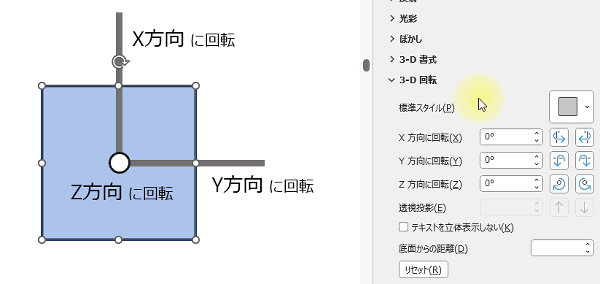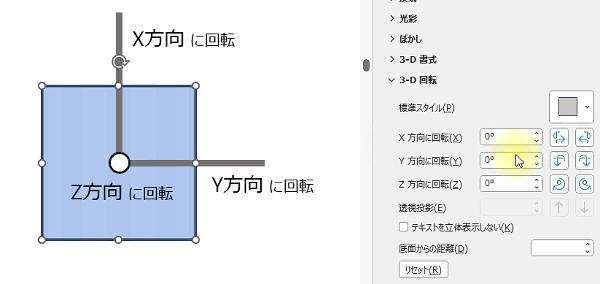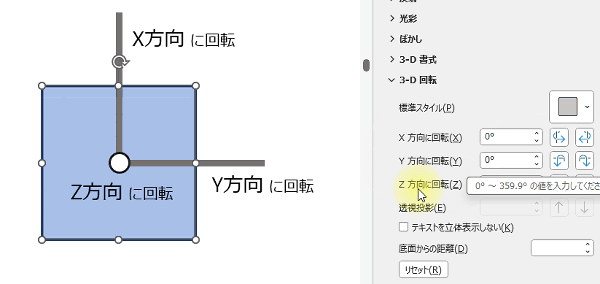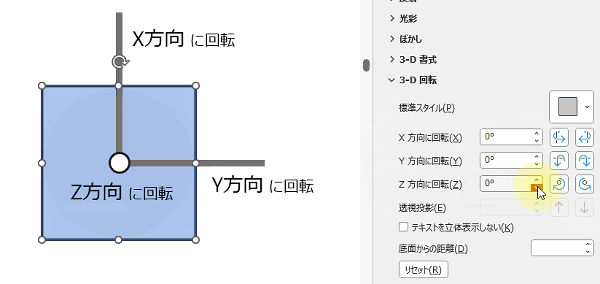
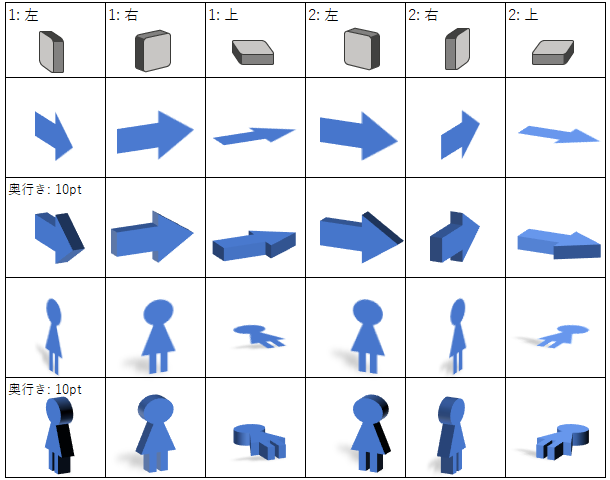
図形を回転する時、X方向、Y方向、Z方向の3方向を指定できます。
X 方向は横回転、Y 方向は縦回転、Z 方向は図形の中心を軸に360度回転します。
「3-D 回転オプション」は、図形を右クリックして[図形の書式設定]をクリックして作業ウィンドウを開き、[図形のオプション]の[効果]タブに切り替えて表示することもできます。
回転サンプル
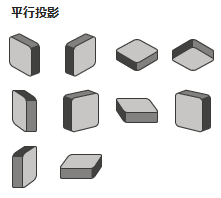
平行投影
等角投影
不等角投影
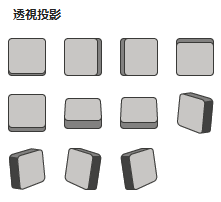
透視投影
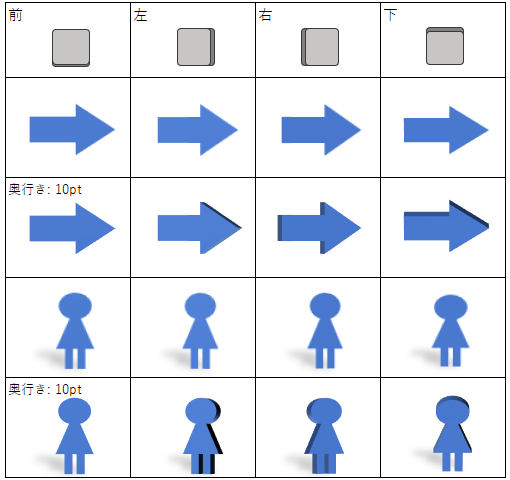

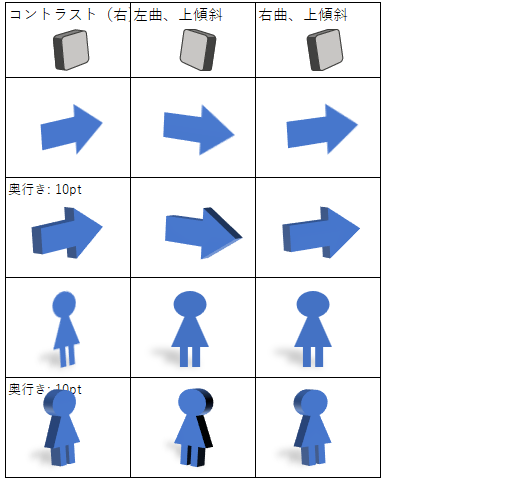
透視投影
[3-D 回転]の設定項目の中で、「透視投影」と書かれている項目は、標準スタイルで透視投影グループの中から回転スタイルを選択した時だけ入力できます。
入力できるのは「0~120度」です。
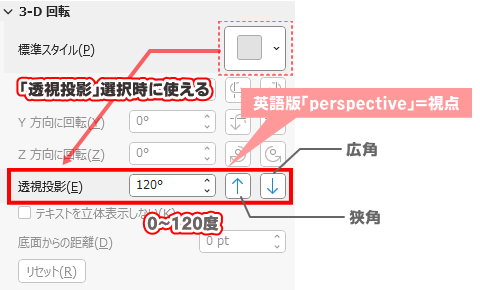
透視投影だけを設定しても変化が分かりにくいので、同じ条件に設定した図形を図法ごとに並べてみました。

テキストを立体表示しない
テキストを入力している図形を[3-D 回転]すると、デフォルトではテキストも一緒に回転します。
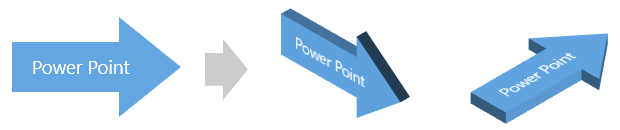
[3-D 回転]オプションの「テキストを立体表示しない」にチェックを入れると、テキストは回転しなくなります。
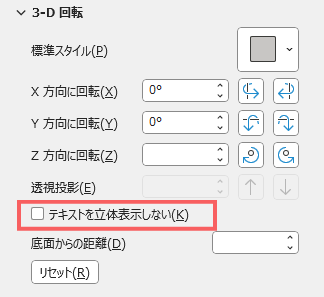

底面からの距離
下図のアイコンは、赤い水平線に対して全て違う位置に立っているように見えますね。
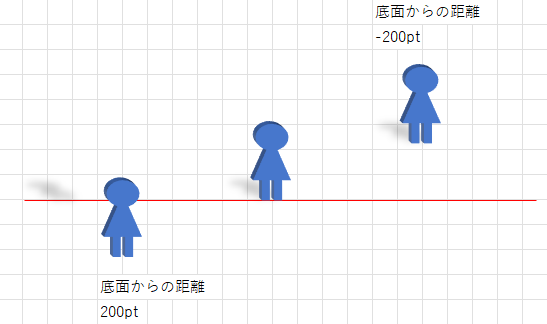
実際には、全て赤い水平線を基準に[下揃え]で配置しています。
なんで違うように見えるかと言うと、左のアイコンには底面からの距離を「200pt」、右のアイコンには底面からの距離を「-200pt」と指定しているからです。
図形を選択してみると、本来の位置が分かりやすくなります。
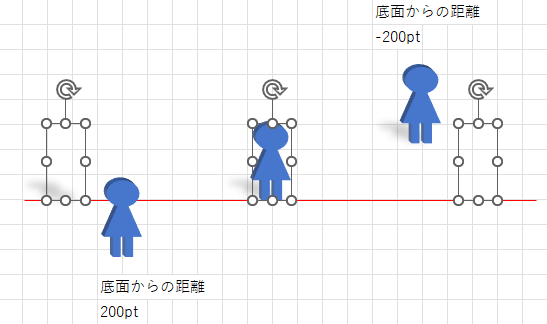
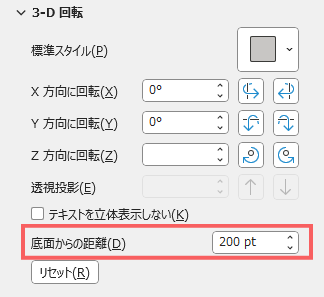
底面からの距離を「-4000pt ~ 4000pt」の値を入力できます。
「底面」は、回転角度によって基準値が変わります。
こんな時に使ってみる?
図形を組み合わせて家イラストを作りました。
奥行きを追加した複数の家を並べて[3-D 回転]を加えると、家の間に空間が生まれてしまいました。

図形を移動すれば綺麗に並んだように見えますが、当然[回転なし]にすると配置がズレています。

底面からの距離を移動したものなら、図形そのものの配置は変化していません。

[3-D 回転]を使って作れるイラスト
ここまでにご紹介した[3-D 回転]をどんな時に使えばいいのか?というヒントになるのではないかと思い、サンプルをご用意しました。
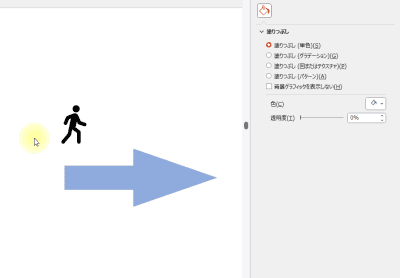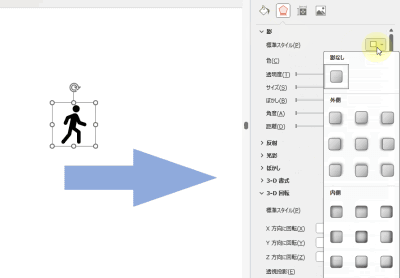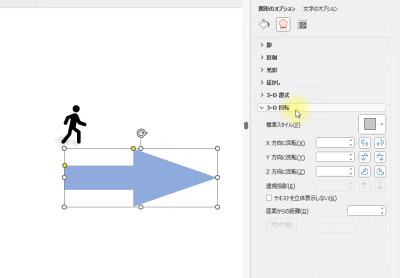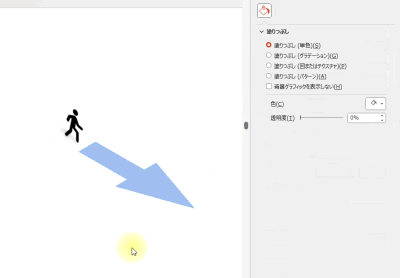
矢印を使った抽象イラスト
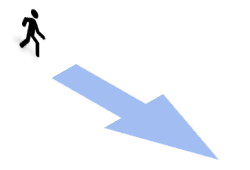
アイコンと図形の矢印ブロックを用意し、[3-D 回転]で回転するだけで、奥から手前に進むインパクトのある矢印に変えられます。
立体地図

[3-D 回転]を使えば、立体感のある地図を作るのも意外と簡単です。
用意するのは、三角形、長方形、道路の数だけの直線です。

三角形と長方形を組み合わせて家の形を作り、グループ化しておきます。
道路も、まずは正面から見た状態で井桁に配置し、グループ化しておきます。ここまではいつもと同じですよね?
あとは、それぞれを[3-D 回転]させるだけです。
サンプルで使用した設定内容は、次の通りです。
- 道路は「等角投影: 上]に回転。
- 家イラストは「等角投影: 左下」に回転。
- 家イラストに[3-D 書式]で奥行きを「10pt」に設定して立体化。
- その他、必要な数の家を複製し、配置場所に合わせて[3-D 回転]。
全ての配置を調整したら完成です。
図形を立体化する方法の詳細は、次の記事をご覧ください。